waves at waves....

From mathematical point of view most primitive (or fundamental) wave is harmonic (sinusoidal) wave which is described by the equation f(x,t) = Asin(wt-kx)), where A is the amplitude of a wave - a measure of the maximum disturbance in the medium during one wave cycle (the maximum distance from the highest point of the crest to the equilibrium). In the illustration to the right, this is the maximum vertical distance between the baseline and the wave. The units of the amplitude depend on the type of wave — waves on a string have an amplitude expressed as a distance (meters), sound waves as pressure (pascals) and electromagnetic waves as the amplitude of the electric field (volts/meter). The amplitude may be constant (in which case the wave is a c.w. or continuous wave), or may vary with time and/or position. The form of the variation of amplitude is called the envelope of the wave.

The wavelength (denoted as λ) is the distance between two sequential crests (or troughs). This generally has the unit of meters; it is also commonly measured in nanometers for the optical part of the electromagnetic spectrum.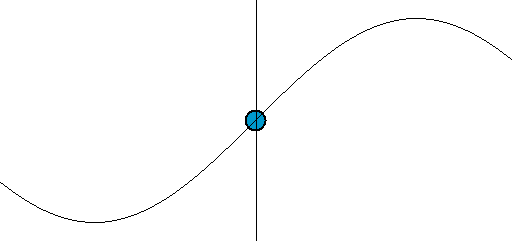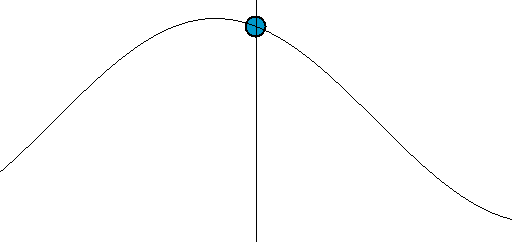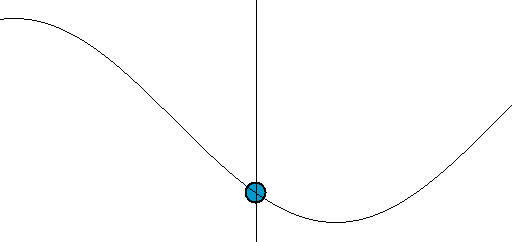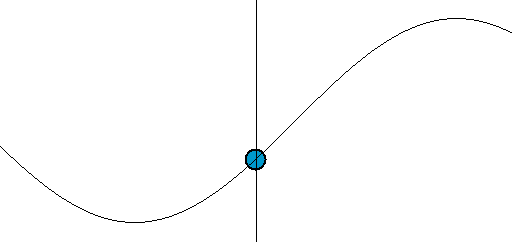

The period T is the time for one complete cycle for an oscillation of a wave. The frequency f (also frequently denoted as ν) is how many periods per unit time (for example one second) and is measured in hertz.

Propagation through strings
The speed of a wave traveling along a string (v) is directly proportional to the square root of the tension (T) over the linear density (μ):