Getting The Resultant Vector

we see 3 vectors with their associated magnitudes and angles. In order to add these, we always must connect vectors 'head to tail' and the resultant vector (which represents the vector sum) is drawn from the tail of the first vector to the head of the last vector (see right side of the diagram below). In this example, using a ruler and protractor, we are able to get a resultant vector of about magnitude 11 and an angle of 102°.In this section, we physically added the vectors by drawing and measuring them. In the real world, we need much greater accuracy.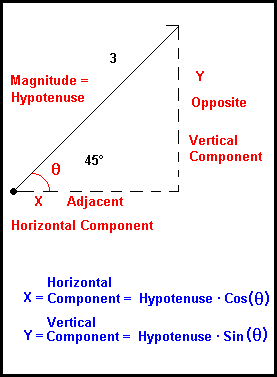

In this section, we will add the same vectors mathematically . To do this, we first must resolve each vector into its horizontal and vertical components. We see from the above formulas that:

X = Horizontal Component = Magnitude * Cos ( q )X= 3 * Cos(45°)X= 3 * 0.707106781186547... = 2.12132034355964 Y = Vertical Component = Magnitude * Sin ( q )Y = 3 * 0.707106781186547... = 2.12132034355964
Moving on to the next vector:X = 6 * Cos(90°) = 0Y = 6 * Sin(90°) = 6
And for the final vector:X = 5 * Cos(150°) = 5 * -0.866025403784439 = -4.33012701892219Y = 5 * Sin(150°) = 5 * .5 = 2.5
Now we sum up the horizontal components (the X values):X sum = 2.12132034355964 + 0 -4.33012701892219 = -2.20880667536255
Summing up the vertical components (the Y values):

Y sum = 2.12132034355964 + 6 + 2.5 = 10.62132034355964
We determine the magnitude of the resultant vector by the Pythagorean Theorem:Magnitude 2 = X2 + Y2Magnitude 2 = -2.208806675362552 + 10.621320343559642Magnitude 2 = 4.87882692912616 + 112.812445840514Magnitude 2 = 117.69127276964Magnitude = 10.848560861683

To determine the direction of the resultant vector the formula is:
ArcTangent (Resultant Vector) = (Ysum / Xsum)
ArcTangent (of Resultant Vector) =10.62132034355964-2.20880667536255)
ArcTangent (of Resultant Vector)= -4.8086237976514
Angle = 101.747770718541 Degrees